Facial recognition technology is on the rise and has already made its way into every aspect of our lives. From smartphones, to retail, to offices, to parks... it is everywhere. If you are just getting started with computer vision, then face recognition is a must do project for you. Here in this guide, I seek to present all the existing facial recognition algorithms and how they work. We will explore classical techniques like LBPH, EigenFaces, Fischerfaces as well as Deep Learning techniques such as FaceNet and DeepFace.
Before we get started, we need to clarify some terminology as people often get confused if they don't understand the nuances.
Face recognition is different from face detection:
There are 2 modes that a face recognition system can operate in:
The list of currently practiced techniques for face recognition are:
Each method lays out a different approach for extracting facial features from the image pixels. Some methods such as Eigenfaces and Fisherfaces are similar. Whereas some are completely non-intuitive to our understanding such as Deep Learning. In this guide, we will try to cover the gist of how each technique works along with links to code examples.
Being one of the easier face recognition algorithms, it is also one of the oldest techniques
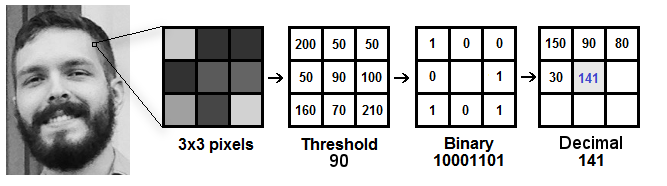
Local Binary Pattern (LBP) is a simple yet very efficient texture operator which labels the pixels of an image by thresholding the neighborhood of each pixel and encodes the result as a binary number.
It was first described in 1994 and has since been found to be a powerful feature for texture classification. As in HOG, we use Histograms to represent and bin the LBP. This allows us to represent the face images with a simple data vector. It has further been determined that when LBP is combined with the histograms of oriented gradients (HOG) descriptor, it improves the detection performance considerably on some datasets. As LBP is a visual descriptor it can also be used for face recognition tasks.
Note: Read more about the LBPH here: http://www.scholarpedia.org/article/Local_Binary_Patterns
Calculation of Local Binary Patterns is done as follows
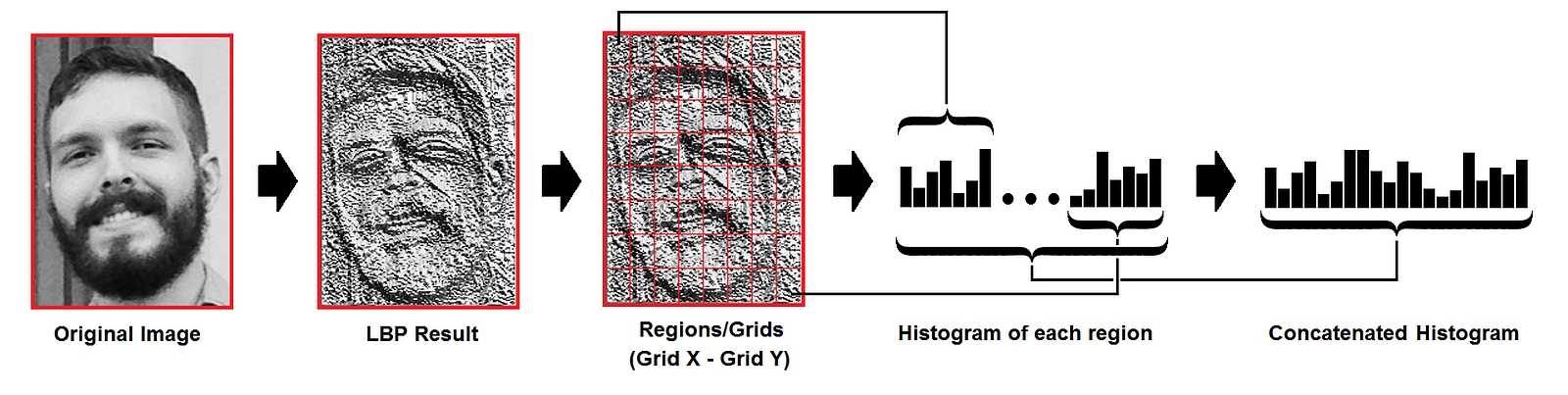
Face images are compared by converting both into LBPH vectors and then calculating the distance between two histograms, for example: euclidean distance, chi-square, absolute value, etc. For ex, Euclidean distance can be calculated based on the following formula:
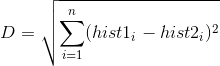
The distance metric can also be thresholded to ensure the match is accurate enough.
One may also train an SVM or Random Forest classifier on a set of these vectors for quick 1vN classification/prediction. This is the LBPH technique in a nutshell.
Eigenfaces is the oldest and one of the simplest face recognition methods. It works quite reliably in most controlled environments and with sufficiently large datasets.
In Eigenfaces algorithm, we "project" face images into a low dimensional space in which they can be compared efficiently. The assumption is that intra-face distances (i.e. distances between images of the same person) will be smaller than inter-face distances (the distance between pictures of different people) in the low dimensional space. This projection of the face on to a lower dimension is a form of feature extraction - the dimensions of this space correspond to a feature. Howerver, unlike standard feature extraction with a fixed extractor, for Eigenfaces we learn the feature extractor from the image data. Once we've extracted the features, classification can be performed using any standard technique. 1-nearest-neighbour classifiers are the standard choice for the Eigenfaces algorithm.
The lower dimensional space used by the Eigenfaces algorithm is learned through a process called Principle Component Analysis (PCA). PCA is an unsupervised dimensionality reduction technique.
The PCA algorithm finds a set of orthogonal axes (i.e. axes at right angles) that best describe the variance of the data such that the first axis is oriented along the direction of highest variance.
Fisherface is a technique similar to Eigenfaces but it is geared to improve clustering of classes. While Eigenfaces relies on PCA, Fischer faces relies on LDA (aka Fischer's LDA) for dimensionality reduction.
The FLDA maximizes ratio of between-class scatter to that of within-class scatter. It, therefore, works better than PCA for the purpose of discrimination.
The Fisherface is especially useful when facial images have large variations in illumination and facial expression. Fisherface removes the first three principal components responsible for light intensity changes.
Fisherface is more complex than Eigenface in finding the projection of face space. Calculation of ratio of between-class scatter to within-class scatter requires a lot of processing time. Besides, due to the need of better classification, the dimension of projection in face space is not as compact as Eigenface. This, results in larger storage of the face and more processing time in recognition.


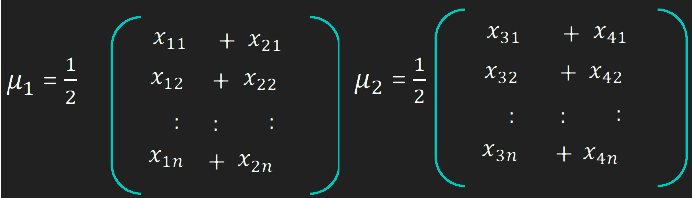
X with each column representing an image. Each image is a assigned to a class in the corresponding class vector C.X into the (N-c)-dimensional subspace as P with the rotation matrix WPcaidentified by a Principal Component Analysis, where
P as Sb = \sum_{i=1}^{c} N_i*(mean_i - mean)*(mean_i - mean)^T, where
mean is the total mean of Pmean_i is the mean of class i in PN_i is the number of samples for class iP as Sw = \sum_{i=1}^{c} \sum_{x_k \in X_i} (x_k - mean_i) * (x_k - mean_i)^T, where
X_i are the samples of class ix_k is a sample of X_imean_i is the mean of class i in PWfld of Sb and Sw corresponding to their eigenvalue. The rank of Sb is atmost (c-1), so there are only (c-1) non-zero eigenvalues, cut off the rest.W = WPca * Wfld.
Fischerfaces yields much better recognition performance than eigen faces. However, it loses the ability to reconstruct faces because the Eigenspace is lost. Also, Fischer faces greatly reduces the dimensionality of the images making small template sizes.
In the next, part of the article we will look into Deep Learning techniques for face recognition.